Experiment: The Scientific Method
Can humans determine the color of Skittles based on taste alone?
Chapter 1: The Scientific Method
Lecture Slides: The Scientific Method
Lecture Video: The Scientific Method
Study Guide: The Scientific Method
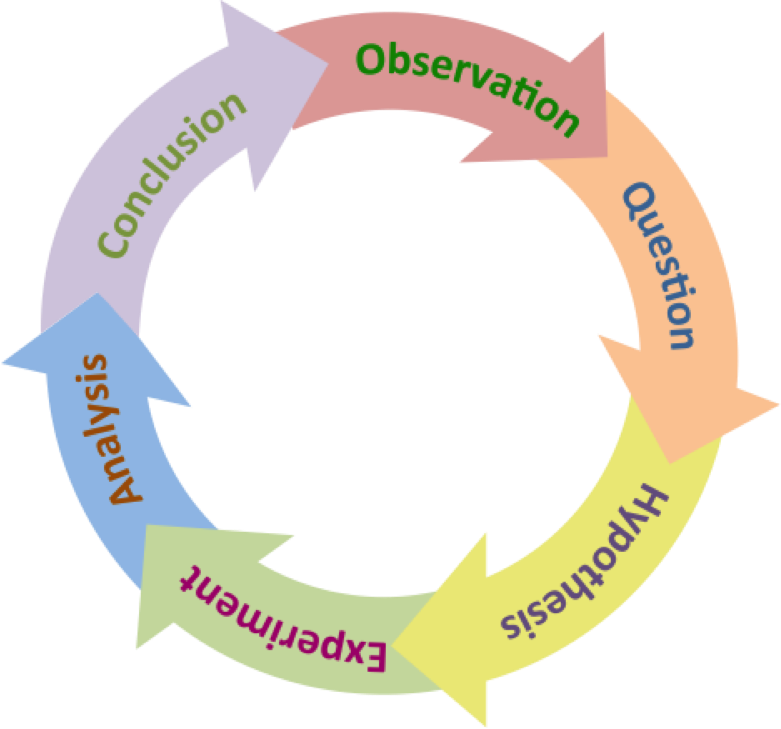
Figure 1. The Scientific Method. Observations of the natural world lead to questions. Scientific questions generate hypotheses, many of which may be tested through controlled experimentation. Experimentation and analysis allows hypotheses to be falsified, which provide information (or conclusions). The process of scientific experimentation leads to more observations and questions.
In this lab, students will use their only their sense of taste to predict the color of Skittles. Once all of the subjects have been tested, the students aggregate their data and use inferential statistics to determine whether or not humans can detect the color of Skittles based on taste alone, in general. Students will also be able to deconstruct the data in order to detect whether people can detect specific colors or not. This lab is fun, yet comprehensive introducing students to the process of the scientific method, including hypothesis generation, data analysis based on statistical inference and hypothesis validation. It is especially useful in online labs, due to the ease of acquiring the materials in the beginning week, and an emphasis on group collaboration and statistical hypothesis testing.
Hypotheses
Typically students are taught that a hypothesis is prediction based on our experience of the natural world. However, in a scientific experiment many different hypotheses are examined during the analysis simultaneously.
Null hypothesis
One possible finding in any experiment, is that we find no statistical difference between (or among) the control group and the experimental group(s). This result would support the null hypothesis (H0), which states that there is no relationship between two measured phenomenon. Referring to the experimental question of this experiment the null hypothesis for this experimental design would be, humans correctly and incorrectly identified the color based on taste alone equally. In other words, there would not be a statistical difference between the average number of correctly predicted observations (i.e. Skittles) and incorrect observation. Or more formally, the null model would be:
H0 : Humans correctly and incorrectly identify the color of Skittles by taste alone with the same frequency.
Alternative hypotheses
If the null hypothesis is rejected, this infers there is a potential relationship between these phenomenon. When this happens, one or more alternative hypotheses (HA) can be proposed to explain the relationship between measured phenomena. Two alternative hypotheses for the proposed null hypothesis are:
If the null hypothesis is rejected, this infers there is a potential relationship between these phenomenon. When this happens, one or more alternative hypotheses (Ha) can be proposed to explain the relationship between measured phenomena. Two alternative hypotheses for the proposed null hypothesis are:
HA1: People correctly identify the color Skittles based on taste alone more often than not.
HA2: People incorrectly identify the color of Skittles based on taste alone more often than not.
Experimental Protocol
If this is an online lab you will perform the following experimental protocol on yourself and one family member or friend at home. If this is a classroom lab, you will work with a group of four to complete this protocol.
- Wash your hands with soap and water.
- Each person (or subject) will receive 3 Skittles of each color (for a total of 15).
- Blindfold the subject.
- The handler will remove the allotted number of Skittles from the package and place them onto a paper plate.
- The handler will give the subject one of the Skittles and the subject will predict its color. The color must be chosen randomly. Do not tell the subject whether the color is correct or not.
- In The Scientific Method Lab of The Biology Lab Primer, record your results. If the color is correctly identified, it is deemed 'correct.' In this case, place a tally under the correct section of that color. If the color is incorrectly identified (or the subject can not identify the color), it is deemed 'incorrect.' In this case, place a tally under the incorrect section of that color. For example, if you select a red Skittle and the subject predicts it is yellow, that is incorrect and you would place a tally under 'incorrect' under 'red.'
- Record your results in the cumulative spreadsheet. For “ALL COLORS” simply add up the tallies of “correct” and “incorrect” for the subject. It is important to note that the more replicates (in our case, subjects tested) the more accurate our results will indicate reality. It is recommended that instructors pool data across multiple classes and provide this data set for the analysis, or provide data to the cumulative spreadsheet above.
- Repeat 4-7 for the other test subject(s). If this is a classroom lab, you will need to test at least two subjects and record your data to your class spreadsheet.
Each subject that you tested in your group is known as a replicate. The more replicates you include in your analysis, the more reliable your findings become. This is due to the fact that certain results can simply happen by chance. For example, if you flipped a coin twice and got heads both times, it does not mean you are certain to get a heads on a third coin toss. For this reason, we are going to collect as possible. Your instructor may choose to have you fill in the table in The Biology Lab Primer with the results from the whole class, reported on the white board (in a face-to-face lab) or in a specific class spreadsheet provided by your instructor (works for face-to-face and online labs), or this cumulative spreadsheet of many classes..
Hypothesis testing
- Go to: http://www.graphpad.com/quickcalcs/ttest1.cfm
- Under “1. Choose data entry format”, select “Enter up to 50 rows.” if inputting a single class's information. If you have been provided a class spreadsheet by your instructor, select "Enter or paste up to 2000 rows." Then copy and paste the appropriate column of observations.
- Under “2. Enter data” you will input your data
- First change the label to correspond with the color of the Skittles and the correctness of the result. For example, if you are testing the means of red Skittles, label group 1 as “Red correct” and group 2 as “Red incorrect”.
- Input the data from those two columns only.
- Under “3. Choose a test”, select “Unpaired t test.”
- Under “4. View the results”, click on “Calculate now.”
- Repeat steps 1-4 for each color (e.g. red, orange, yellow, green, purple), and for “ALL COLORS.”
Figure 2. Decision tree to determine which hypothesis is supported. Once you complete your statistical analysis. If your p value is greater than 0.05, there is an insignificant different between the columns of numbers you are comparing. In this study, it would indicate that the mean (or average) of the two groups (correct and incorrect) are not statistically different from each other. In this scenario, the conclusion would be that the results support the null hypothesis, and the conclusion would be "From this experiment, it can not be determined whether humans can or can not determine the color based on taste." Another way of thinking about this is that people correctly and incorrectly identified the color at approximately an equal rate. If the p value is less than 0.05, this indicates there is a significant difference between the number of Skittles correctly identified and incorrectly identified. This doesn't automatically indicate that people are more likely to correctly identify the color. The next step is to look at the means of the two groups of numbers. If the mean for correct is smaller than the mean for incorrect, this supports the alternative hypothesis, "Humans can not identify the color based on taste alone," indicating people get it wrong more often than they get it right. If the mean for correct is greater than the mean for incorrect, the other alternative hypothesis, "Humans can identify the color based on taste alone."
Analysis
If you have never taken a statistics class before, the results provided by QuickCalcs (GraphPad Software, 2013) might be intimidating. Have no fear! We will just focus on the statistics that will answer our question to tests our hypothesis (see fig. 2).
p value
The p-value allows us to determine whether or not the means of the two samples are “significantly” different. When you take a statistics class, you will learn how this statistic is created. For our purposes, it is sufficient to be able to interpret this statistic without actually knowing how to calculate it. The important thing to note is this value will allow us to determine whether or not the means differ.
The p-value is the probability (ranging from zero to one), which answers whether or not the observed means of two populations (e.g. “correct” and “incorrect” in our study) are real and not merely a product of chance. In most biological studies, if the p-value is less that 0.05 (p<0.05) we can state that there is, in fact, a “statistical” difference between the two populations. This is somewhat of an artificial cut off, but it is one that is widely accepted in this field of study. Therefore, in our study if you get a result of p<0.05, we can conclude that there is a “significant” difference between the “correct” group and the “incorrect” group for that color.
Mean
The mean is an average of a group of numbers. If you find that there is a significant p-value (p < 0.05), then the next step is to look at the means (fig. 2). If the mean is larger for the “correct” group, this means that humans can identify that color by taste alone. If the mean is larger for the “incorrect” group, this means that humans can not identify that color by taste alone. In other words, humans incorrectly predicted the color of Skittles more often than they correctly identified the color.
Results and Conclusion
Once we get our results, we must revisit our hypotheses and either validate them or invalidate them (see fig. 2 above). If the pivalue is insignificant (p > 0.05), the null hypothesis would be supported: It can not be determined whether or not humans can or can not determine the color of Skittles based on taste alone. Another way of saying that is that humans correctly identified and misidentified the color of Skittles at approximately the same rate. If the p-value is significant (p ≤ 0.05), then one of the alternative hypotheses are supported. If the mean for 'correct' is greater than 'incorrect', this would support the alternative hypothesis: Humans can determine the color of Skittles based on taste alone. This means that the subjects correctly identified the color more time that they incorrectly identified it. If the mean for 'incorrect' is greater, the conclusion would be: Humans can not determine the color of Skittles based on taste alone. In other words, the subjects incorrectly identified the color more often than correctly identifying it.
Figure 3. An example of how to report your results on your lab report. Be sure to present your means with bar graphs, including the mean of each group, and write numbers indicating the scale that you used in on the y-a. Record the p value in the upper right corner.
Example Result and Conclusion
Figure 3 represents results that could be found in this experiment for red Skittles. It is comparing the number of correct versus incorrect identification of red Skittles based on taste alone. If we look at the p-value, it is less that 0.05 (0.02 = p < 0.05). From this statistic, we can conclude that there is a difference between the means of "correct" and "incorrect". By comparing the means, we see that the mean "correct" is greater that "incorrect". From this we would support the alternative hypothesis with confidence, Humans can determine the color of red Skittles based on taste alone.
An imperfect experiment
Ideally, an experiment would have a control group and one or more experimental groups. Control groups have none of the treatment or the standard treatment, whereas experimental groups have the treatment. In medical experiment, the control group typically includes subjects that do not receive the treatment (i.e. medical procedure or medicine). Control groups are important so that the effect of the experimental treatment can be calibrated and accurately measured. Many experiments have multiple experimental groups, which include the different amounts of the treatment. In medicine, this is a common attribute of experiments to test the best appropriate dosage of a medicine.
This particular 'experiment' is really more of an observational study and less of an experiment because there is really no control or experimental group. A potential way to make this observational study better (notice I didn't use 'experiment'), would be to split the subjects in the experiment into two groups. Humans have a bias in their ability to determine the color of Skittles. Some people eat Skittles daily, others can not stand the taste of them and may have not eaten them in years. A scientist could predetermine the frequency which the subjects eat Skittles. Those that eat them most frequently (say weekly), could be placed in one group. Those that eat them monthly in a different group, and those that eat them infrequently in a third group. In this study, we would be able to ask more a nuanced question: Does the frequency in which people regularly eat Skittles determine their ability to detect their color from taste alone? However, there still really isn't a treatment, and therefore isn't a control group. Would those that eat them most frequently be the control group or those that eat them infrequently. While this isn't a perfect experiment, it remains a valid scientific endeavor as it does give us information about the natural world.
Copyright © 2016 Jason S. Walker. All rights reserved.